V Oscillations des plasmas

Lorsqu’un excédent de charges est fourni à un plasma, sous la forme d’une augmentation du nombre d’électrons ou d’ions, celui-ci tend à retrouver un état macroscopiquement neutre. Pour cela, les électrons vont se déplacer des lieux les plus négatifs vers les plus positifs (les ions étant beaucoup plus lourds que les électrons, ils auront une vitesse négligeable à côté de celle des électrons). Durant ce mouvement, ils acquièrent une énergie cinétique suffisante pour franchir l’état d’équilibre. De ce fait, des oscillations pendulaires non amorties de charge vont se produire autour de l’état d’équilibre de neutralité dans le plasma. Les premières observations du phénomène d’oscillation de plasma ont été faites par F.M. Penning et ont été plus profondément étudiées par L.Tonks et I.Langmuir.

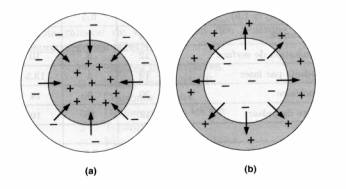
Schéma des oscillations

On voit par exemple sur le schéma a. l’effet produit par un excédent d’électrons sur la partie extérieure. La partie intérieure est alors globalement plus positive que l’extérieure, ce qui crée un champ électrique tendant à attirer les électrons au centre. Ils acquièrent alors une énergie cinétique pour dépasser l’état d’équilibre. On a alors une situation assimilable à la figure b., où la charge globalement positive est portée par la périphérie, qu’un trop grand nombre d’électron a quittée, rendant du même coup la partie interne globalement négative. Les mêmes mouvements vont alors recommencer dans l’autre sens, dans des oscillations pendulaires non amorties. La force s’exerçant sur chaque électron étant F :

on trouve en appliquant la R.F.D. : (les calculs sont explicités dans l’exemple des oscillations de gaine)

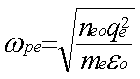
où est la charge de l’électron, la densité du plasma non perturbé. La fréquence plasma est alors

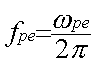
ou plus simplement en remplaçant les constantes par leurs valeurs approchées,

Quelques fréquences plasma ont étés reportées dans le tableau ci dessous :

PLASMAS USUELS	Log()	Log(Te)	Log(fpe)	Log()
Gaz faiblement ionisés
Ionosphère, couche D, altitude 70 km	3	2.5	7.5	0.5
Décharge dans les gaz-courant faible	11	4	9.5	-3
Décharge dans les gaz-courant fort	15	5	11.5	-4
Convertisseur M.H.D.	16	3	12	-6
Gaz fortement ionisés
Gaz interstellaire	0	3.5	4	2.5
Vent solaire	0.5	5	4	3
Ionosphère, couche F, altitude 250 km	5.5	3	7	-0.5
Couronne solaire (R1.6)	7	6.5	7.5	0.5
Plasmas de tokamak	14	7	11	-3
Plasmas d’ionisation de surface	12	3	10	-4
Plasmas produits par laser	19	5	13.5	-6
Explosion nucléaire	20	6	14	-6
Magnétosphère de pulsar	12	16	10	3
Matière dense
Electrons dans les métaux	23	2.5	15.5	-9.5
Intérieur des étoiles	27	7.5	17.5	-9.5
Intérieur des naines blanches	32	7	20	-12

T_e est la température électronique du plasma.

Toutes les mesures ont été effectuées dans le système C.G.S. correspondant au cm, au gramme, et à la seconde.

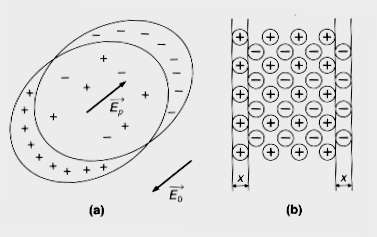
Oscillations de gaine

On peut observer des oscillations de plasma dans d’autres cas. Par exemple, lorsqu’on expose un plasma borné, nettement limité du vide, à un champ électrique perpendiculaire à la frontière, on observe un déplacement des électrons par rapport aux ions, qui vont alors prendre la position représentée sur le schéma a. des oscillations de gaines. Il se forme alors à la frontière du plasma une gaine d’électrons ou de cations selon le sens du champ (schéma b.). Les deux parties externes du plasma créent alors un champ de polarisation annulant le champ extérieur. Si on cesse alors brusquement l’action du champ extérieur, le plasma va tendre à retrouver sa position initiale d’équilibre. On aura alors à nouveau des oscillations autour de cet état d’équilibre, dépassé à cause de l’énergie cinétique. Dans le cas d’une lame plane de plasma, on peut calculer le champ de polarisation  :

où est la densité superficielle de la partie positive ou négative dépassant du plasma.

C’est à dire :

donc le champ vaut :

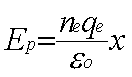
Et les électrons sont donc soumis à la force de rappel F :

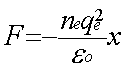
L’équation différentielle gouvernant les oscillations est donc :

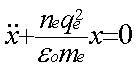
On retrouve donc l’équation d’oscillations pendulaires non amorties, appelées oscillations de gaine, dans laquelle on retrouve la pulsation  valant exactement la pulsation de la fréquence plasma :

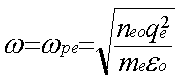
Pour des plasmas dont les formes sont différentes, on a un facteur numérique A, valant par exemple pour un cylindre, ou pour une sphère.